연습문제    [DOC]    [SMTS]

1. 화면에 자신의 학번과 영문 이름을 출력하는 프로그램을 작성하라.

2. 화면에 다음과 같이 출력하는 프로그램을 작성하라

----------------------

1 2 3

one two three

uno due tre

---------------------

(3)  (110101.11)2를 10진수와 16진수로 변환하라.

(4) 십진수 625를 2진수와 16진수로 변환하라.

(5) 십진수 0.6825를 2진수로 변환하라.

2.7 논리형 (bool 형)    [DOC]    [SMTS]

 논리형(bool type)은 진리값인 참/거짓을 표현하는 자료형을 의미한다. ANSI C에서는 부울형이 따로 지정되지 않았지만 C99에는 stdbool.h 헤더파일을 이용하여 bool형을 사용할 수 있다.

참을 나타내는 true와 거짓을 나타내는 false 식별자는 내부적으로 각각 1과 0값으로 취급된다.

 C++에서는 boolean 형이 기본 자료형으로 제공된다. 따라서 별도의 헤더파일을 인클루드하지 않고 바로 부울형 변수를 정의하여 사용할 수 있다.

표 2.3.1 문자와 ASCII 코드

char형은 크기가 1바이트이므로 부호 없는 unsigned char 변수인 경우 0부터 255까지의 작은 정수를 저장할 수 있으며 short형은 2바이트로 부호 없는 숫자의 경우 0부터 65,535까지 저장할 수 있다. 만약 char형 변에 문자상수, 예를 들어서 ‘a’가 저장되면 내부적으로는 97이라는 숫자가 저장된다는 것을 알아야 한다.

[표 2.3.2 ] 한 문자가 저장되는 비트 구조

부호가 있는 정수형 데이터는 음수를 2의 보수로 저장하기 때문에 저장범위가 char형은 –128 ~ +127이 되고 short형은 –32,768 ~ +32,767이 된다.

 다음 예를 컴파일한 후 실행해 보자.

이것을 보면 문자 ‘a’는 내부적으로 97, ‘A’는 65, 그리고 문자 ‘0’은 48과 같다는 것을 알 수 있다.

 실수를 표현할 때는 0.1, -2,3 과 같은 보통의 10진 표기법 외에 지수적 표기법이라는 것이 있는데 예를 들면1.234567e5 와 같은 것이다. 이것은 과학적 표기인

를 표현한 것이다. 또 다른 예로 1.234567e-3 은

이다. 실수 상수는 소수점을 반드시 포함해야 하며 지수부는 생략할 수 있다. 예를 들면 다음과 같다.

실수형 변수를 선언하고 초기화하는 코드의 예는 다음과 같다.

 실수 자료형은 float형, double형, long double형이 있는데 float형보다 double형의 표현 범위뿐만 아니라 정밀도도 더 높다. (정수형은 예를 들어 short형 보다 long형이 표현 범위만 넓어지는 것과 대조적이다)

 실수 상수는 내부적으로 double형으로 저장되므로 8 byte 메모리가 소요된다. 만약 실수 상수를 float 형으로 명시적으로 지정하려면 숫자 뒤에 f/F 접미어를 붙이면 된다.

하지만 이 경우에도 자동으로 형 변환이 일어나므로 궂이 f/F 접미어를 붙여줄 필요는 없다.

 이와 같이 변수에 숫자상수를 대입할 경우에는 묵시적으로 형변환이 일어나기 때문에 사용자는 특별한 경우를 제외하고는 신경을 쓸 필요가 없다.

 예를 들어 부호가 있는 int 형 변수 ia 를 숫자 0으로 초기화하려면 다음과 같이 하면 된다.

이후에는 ia라는 int형 변수를 '사용'하여 정수 값을 저장하거나 산술 연산을 수행할 수 있다.

 C언어에서 정수를 표현할 때 0으로 시작되는숫자는 8진수이고, 0x로 시작하는 숫자는 16진수라는 것이다. 예를 들어서 123은 그냥 10진수 123이지만 0123 이라고 입력하면 8진수 123이기 때문에 10진수로 변환하면 83이다. 그리고 0x123은 16진수 123이기 때문에 10진수로 변환하면 291이 된다. 이것을 다음 표에 정리하였다.

[표 2.2.1] 숫자상수의 접두어 예

0123의 경우 십진수 123이라고 오해하기 쉬운데 0으로 시작하는 수는 8진수로 간주된다는 사실을 유의해야 한다.

 다음 예를 실행시켜보자.

이 결과로부터 8진수 123은 십진수 83이고 16진수 123은 십진수 291과 같다는 사실을 알 수 있다.

 정수형 상수는 기본적으로 int형으로 간주되므로 내부적으로 저장하는데 4 byte(혹은 2 byte)가 소요가 된다. 만약 숫자 상수를 특정한 자료형으로 지정해 주고 싶다면 접미어를 붙여서 그 데이터형을 지정할 수 있는데 U(혹은 u)를 붙이면 unsigned int형이고 l(혹은 L)은 long형, ul(혹은 UL)은 unsigned long형임을 나타낸다.

표 2.2.2 숫자상수의 자료형을 지정하는 접미어들

예를 들면 다음과 같다.

하지만 보통은 숫자 상수는 대입하려는 변수의 자료형에 자동으로 변환되어 저장되므로 굳이 이렇게 일일이 자료형에 맞추어 접미어를 붙여줄 필요는 없다. 즉,

이라고 초기화하여도 123이라는 int형 상수는 자동으로 unsigned long 형으로 변환된 후 변수 ula에 저장된다.

 만약 숫자상수를 short 형이나 unsigned char 형으로 지정하고 싶다면 다음과 같이 해야 한다.

이와 같이 숫자 상수 앞에 (자료형)을 붙여 자료형을 강제로 변환하는 것을 형변환(casting)이라고 한다. 하지만 이 경우도 아래와 같이 할 수 있다.

이렇게 해도 자동으로 형변환이 일어나기 때문에 문제가 없다.

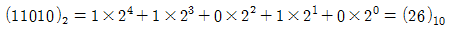
비트가 0일 때는 10진수로 변환하는 합에 영향을 미치지 않는다. 그러므로 10진수로의 변환은 비트가 1인 2의 거듭제곱수의 합으로 얻을 수 있다. 예를 들면 다음과 같다.

1.9.2 16진수

 16진수를 사용하여 2진수를 더 간결하게 표현하는 것이 길이가 4배 더 긴 2진으로 된 비트열을 사용하는 것보다 훨씬 편리하다. 그러므로 디지털 시스템에서는 2진수를 기술하기 위해 16진수를 많이 사용한다.

 16진수는 15까지 한자리로 표현되고 16이 되면 두 자리로 넘어간다. 따라서 10진 시스템에서 가져온 10개의 숫자와 10, 11, 12, 13, 14, 15를 하나의 숫자로 표현하기 위해 사용되는 문자 A, B, C, D, E, F를 갖는 기수 16 시스템이다. 16진수에 대한 예는 다음과 같다.

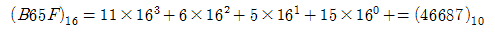
다음 표에 16진수 0부터 15까지를 2진수와 8진수로 표현한 것을 기술하였다.

[표 1.12.2]  

이중에서 2진수와 16진수와의 관계는 눈여겨 보아야 한다. 2진에서 16진수로의 변환은 2진 숫자를 소수점부터 시작하여 왼쪽과 오른쪽으로 4비트씩 나눔으로서 쉽게 얻어진다.

1.9.3 10진수로의 변환

 10진수에서 2진수로 변환하는 편리한 방법은 주어진 10진수를 반복해서 2로 나누어서 그때마다 나머지를 써두고, 그 몫을 다시 2로 나누는 방법을 몫이 0이 될 때까지 반복한 후 아래에서부터 위로 나머지를 읽어가는 방법이다. 예를 들어 10진수 103을 2진수로 변환하면 다음과 같다.

따라서 (103)10=(1100111)2 가 된다.

 이번에는 (0.125)10 처럼 10진수의 소수값을 2진수로 변환시키는 방법을 알아보자. 주어진 소수값에 2를 곱한다음 그 결과값이 1을 넘으면 1을 써두고 1을 넘지 않으면 0을 써둔 다음 그 너머지 소수값에 다시 2를 곱한다. 이것을 소수값이 없어질 때까지 반복한 다음, 써둔 결과를 위에서 부터 읽어 내려간다. 즉,

따라서 (0.125)10=(0.001)2이다.

 10진수에서 8진수 혹은 16진수로의 변환도 8 혹은 16으로 나누고 곱한다는 것만 빼고 위와 동일하게 얻어진다.

1.9.4 보수 (선택 사항)

 디지털시스템(digital system)에서는 음수를 표현하기 위해서 2의 보수(2‘s complement)를 사용한다. 1의 보수(1’s complement)는 0과 1을 서로 바꾸어서 얻을 수 있다. 즉 0→1, 1→0으로 변환하는 것이다. 예를 들어서

 n개의 자리수를 가진 2진수 N이 주어지면 2의 보수는 N≠0일 때 2n-N이고 N=0일 때 0으로 정의한다. 2의 보수는 1의 보수에 1을 더하여 얻을 수 있다. 예를 들어

또한 2의 보수는 최하위자리 0과 첫 번째 자리 1을 모두 변하지 않게 하고 다른 모든 상위자리 비트에 있는 1을 0으로, 0을 1로 바꾸어 만들 수 있다. 그래서 (1101100)2의 하위 자리수에 있는 2개의 0과 첫번째 1을 그대로 두고 다른 4개의 상위자리의 비트를 0을 1로 1을 0으로 바꾸어서 (0010100)2를 얻을 수 있다. 보수의 보수가 원래의 값을 갖는다는 것도 중요한 사실이다.

앞에서도 밝혔듯이 디지털 시스템에서는 2의 보수로서 음수를 표시한다. 예를 들어 8bit 숫자 체계에서 -10을 얻으려면 +10의 2의 보수를 구하면 된다. 즉 의 2의 보수인 이 -10이 되는 것이다. 이러한 개념은 감산 하드웨어를 간략하게 하는데 매우 유용하다.

[표 1.12.3] 8비트 수의 2의 보수

1.9.5 디지털 데이터 단위

 디지털 시스템에서 모든 데이터는 2진수로 표시된다. 2진수에서 각 자리의 수를 비트(bit)라고 하는데 이것이 디지털 데이터의 최소 단위이다. 2진 신호가 몇 개가 묶였느냐에 따라서 다음과 같이 구분한다.

• 비트 (bit) : 0/1을 표시하는 최소 데이터 단위

• 니블 (nibble) : 4 bits

• 바이트 (byte) : 8 bits

• 워드 (word) : 2 bytes = 16 bits

• 더블 워드 (dword) : 2 words = 4 bytes = 32 bits

 다음 표에 220 까지의 십진수를 나열하였다. 이 중에서 210까지는 외우는 것이 앞으로 프로그래밍하는데 있어서 여러모로 편리하다.

[표 2.12.1] 2의 거듭제곱

또한 8자리 2진수의 최대값은 255, 16자리 2진수의 최대값은 65,535 라는 것도 알아두면 나중에 C언어 변수의 가용 범위를 계산할 때 유용하다.

 디지털 데이터의 용량을 표기할 때 물리적인 단위와는 다소 다르다.

• 킬로(kilo) : 210 = 1,024

• 메가(mega) : 220 = 1,048,576

• 기가(giga) : 230 = 1,073,741,824

• 테라(tera) : 240 = 1,099,511,627,776

예를 들어서

이다.

1.8 atom 에디터 설치 / 첫 프로그램 실행하기    [DOC] [SMTS]

 프로그램을 입력하기 위해서는 에디터가 필요하다. 편집/저장 기능이 있는 프로그램을 아무 것이나 사용해도 상관없으나 본 교재에서는 atom이라는 에디터를 사용하기로 한다. 이 에디터는 프로그램 저장소로 유명한 github에서 만들어서 무료로 사용할 수 있도록 배포되고 있다. 이 프로그램도 choco 명령어를 이용하면 쉽게 설치할 수 있다. 단, .NET framework 4.5 이상이 사전에 설치되어 있어야 한다.

만약 .NET framwork 이 설치되어 있지 않다는 오류가 난다면 atom.io 에서 윈도우용 인스톨러를 다운로드 받아서 설치하는 것이 더 편리하다.

[그림 1.7.1] atom.io 홈페이지. 인스톨러를 다운로드 받을 수 있다.

설치가 끝난 후 윈도우버튼을 확인해 보면 atom 아이콘이 보일 것이다. 이것을 실행하면 된다.

[그림 1.7.2] atom 에디터의 외형

atom 에디터는 컴파일러는 포함되어 있지 않지만 프로그래밍에 유용한 여러 최신 기능들과 플러그인을 무료로 사용할 수 있다. 또한 맥과 리눅스 용도 있어서 한 번 익혀 놓으면 실행 환경이 바뀌더라도 동일한 UI로 사용할 수 있다는 장점도 있다.

 이제 텍스트 에디터를 이용하여 새로운 파일을 생성하여 다음과 같은 프로그래밍을 작성한 후 저장해 보자.

그 다음에 콘솔창에서

라고 입력하면 링크/컴파일이 수행되고 a.exe 실행파일이 생성된다. 이 실행파일을 실행하면 화면에 “Hello world!”가 출력되는 것을 확인할 수 있다.

 이 프로그램에서 다른 부분은 차차로 설명하기로 하고 printf(...) 는 화면에 문자열을 출력하는 함수라는 것만 알아두자. 문자열은 큰따옴표 “...”로 묶은 문자들의 집합을 의미한다. 따라서 printf(“Hello world!\n”) 은 “Hello world!\n”이라는 문자열을 화면에 표시하는 일을 수행한다.

1.7 윈도우즈에 mingw 설치    [DOC]    [SMTS]

 윈도우즈에서 실습을 진행하기 위하여 무료로 사용할 수 있는 gcc 컴파일러를 사용하고자 한다. gcc는 리눅스 응용 프로그램 개발에 사용되는 C 컴파일러이므로 우분투와 같은 리눅스 시스템에서는 바로 사용하는데 아무런 문제가 없다. 만약 윈도우즈를 사용한다면 gcc를 윈도우즈에서 사용할 수 있도록 해주는 mingw 패키지가 있으므로 이것을 설치하여 사용하면 된다.

1.7.1 tdm-gcc 설치하기

 윈도우즈에서  mingw를 설치하는 가장 간단한 방법은 tdm-gcc 를 다운로드 받아서 설치하는 것이다. 자신의 윈도우가 32bit 인지 64bit 인지를 확인한 후 해당 버전의 설치판을 다운로드 받아서 설치하기만 하면 된다.

1.7.2 chochlatey 이용하기

 윈도우즈에서 mingw를 설치하는 다른 방법은 chocolatey 라는 윈도우 패키지 매니저를 사용하는 것이다. 다음과  같이 [windows키]+[R]을 누른 후 ‘cmd’를 입력한 후 [ctrl]+[shift]+[enter] 키를 누른다. 그러면 관리자모드로 명령창이 실행된다.

[그림 1.7.1] cmd 실행 창

여기서 chocolatey 홈페이지에 있는 설치 명령을 복사해서 실행시키면 쉽게 설치할 수 있다.

 chocolatey가 설치된 이후에는 choco라는 명령어를 명령창에서 사용할 수 있다. 정상적으로 설치되었다는 것을 확인하고 싶다면 그냥 choco라고 입력하면 chocolatey의 버전이 출력된다.

이제 mingw를 다음과 같이 설치할 수 있다.

 어떤 방법으로든 mingw가 정상적으로 설치되었다면 c:\tdm-gcc\mingw32 혹은 c:\tools\mingw32 폴더가 생성되고 그 안에 필요한 파일들이 복사되어있을 것이다. 이제 명령창을 다시 실행시키면 gcc 를 실행시킬 수 있다.

위와 같이 출력되었다면 이제 gcc 컴파일러를 사용할 준비가 된 것이다.

1.7.3 컴파일 환경 설정

 본 교재에서는 c99 표준을 기준으로 기술되었다. 따라서 gcc를 이 표준에 맞추어 C코드를 컴파일 하도록 하려면 -std=c99 라는 옵션을 주어야 한다. 컴파일을 수행할 때마다 매번 입력하기 번거로우므로 c:\tools\mingw32\bin 폴더 안에 다음과 같은 배치파일을 작성하여 넣어 두자.

이제 gcc명령 대신 cc명령으로 C99표준에 맞추어 C프로그램을 컴파일 할 수 있다.

 실습을 위해 별도의 폴더를 하나 생성하여 cmd를 실행할 때마다 그 폴더에서 시작하도록 설정하는 것이 앞으로 실습을 진행하는데 편리하다. 예를 들어 d:\cprog 라는 폴더를 만들고 모든 예제를 이 폴더에 저장하여 실행하고 싶다면 c:\windows\system32\cmd.exe 파일을 찾아서 바탕화면에 단축아이콘을 등록한다. 단축아이콘에서 마우스 오른 버튼을 눌러 속성창을 띄우면 시작 위치를 입력하는 곳이 있다.

[그림 1.7.2] cmd 속성창

그리고 단축키(예를 들어 ctrl+shift+c)를 지정해 놓으면 손쉽게 지정된 폴더에서 시작하는 cmd창을 실행시킬 수 있다.

1.1 프로그래밍 개요     [DOC]    [SMTS]

 근래에 들어서 전 세계적으로 소위 코딩(coding)에 대한 관심이 높아지고 있으며 우리나라도 코딩 교육의 중요성을 인식하고 중등 학생들도 관련 과목이 정규 교과에 반영되도록 하는  여러 정책들이 만들어지고 있다.

 코딩이란 컴퓨터가 주어진 일을 수행하도록 프로그램(program)을 작성하는 것을 말한다. 프로그램이란 인간이 작성하고 기계(주로 컴퓨터와 같은 디지털 시스템)가 해독하여 실행할 수 있는 문서이다. 프로그램을 작성하는 문법을 정한 규약을 프로그래밍 언어(programming language)라고 한다. 본 교재에서 다루는 C 언어도 다양한 프로그래밍 언어 중 하나이다.

• 코딩 : 컴퓨터가 주어진 일을 수행하도록 프로그램(progrma)을 작성하는 것

• 프로그램 : 인간이 작성하고 기계(주로 컴퓨터와 같은 디지털 시스템)가 해독하여 실행할 수 있는 문서

• 프로그래밍 언어 : 프로그램을 작성하는 문법을 정한 규약

[그림 1.1.1] 현대의 디지털 시스템의 예

 프로그램이 필요한 대상은 작은 마이크로컨트롤러(micro-controller) 시스템부터 소형 임베디드 시스템(embedded system), 스마트폰, 태블릿, 컴퓨터, 서버, 데이터 센터 등 그 폭이 매우 넓다. 현대의 인간이 생활하는데 필수 불가결한 시스템들이 모두 프로그램에 의해서 동작하고 있으며 따라서 코딩하는 기술은 매우 중요할 뿐만 아니라 새로운 산업까지 일으킬 수 있는 부가가치가 높은 영역으로 인식되고 있다.